第 2 問 論理関数の標準形と単純化 (合計 20 点)
次の二次元の真理表が四つの論理変数 A, B, C, D の論理関数を定義する。
|
A |
T |
T |
F |
F |
| B |
T |
F |
T |
F |
| C |
D |
|
|
|
|
|
| T |
T |
|
T |
T |
T |
F |
| T |
F |
|
T |
T |
T |
F |
| F |
T |
|
T |
T |
T |
F |
| F |
F |
|
T |
T |
F |
F |
2.1 以上の論理関数を標準形で表しなさい
(ヒント: 加法標準形か乗法標準形か短い方を選んだ方がいい) (10 点)
(A∨¬B∨C∨D) ∧
(A∨B∨¬C∨¬D) ∧
(A∨B∨¬C∨D) ∧
(A∨B∨C∨¬D) ∧
(A∨B∨C∨D)
2.2 以上の論理関数に相当する式を単純化しなさい
(ヒント: カルノー図表を使っても良いが、その結果をできればもっと単純にしなさい) (10 点)
(A∨¬B∨C∨D) ∧ (A∨B∨¬C∨¬D) ∧ (A∨B∨¬C∨D) ∧ (A∨B∨C∨¬D) ∧ (A∨B∨C∨D)
(A∨¬B∨C∨D) ∧ (A∨B∨¬C∨¬D) ∧ (A∨B∨¬C∨D) ∧ (A∨B∨C)
(A∨¬B∨C∨D) ∧ (A∨B∨¬C) ∧ (A∨B∨C)
(A∨¬B∨C∨D) ∧ (A∨B)
A ∨ ((¬B∨C∨D) ∧ B)
もっと単純: A ∨ (B ∧ (C ∨ D))
第 3 問 関係の表現、性質と組み合わせ (合計 24 点)
次の行列で関係 R が定義される。
|
A |
B |
C |
D |
| A |
T |
T |
F |
F |
| B |
F |
T |
T |
F |
| C |
F |
F |
F |
F |
| D |
F |
F |
T |
F |
3.1 R を有向グラフで表現しなさい (8 点)
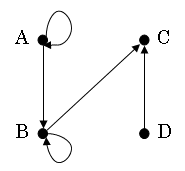
3.2 R∘R を計算して、行列として表しなさい (8 点)
|
A |
B |
C |
D |
| A |
T |
T |
T |
F |
| B |
F |
T |
T |
F |
| C |
F |
F |
F |
F |
| D |
F |
F |
F |
F |
3.3 R と R∘R
の二つの関係について性質の真偽を判断し、記述しなさい (8 点)
| 関係 |
反射的 |
対称的 |
推移的 |
反対称的 |
|---|
| R |
F |
F |
F |
T |
|---|
| R∘R |
F |
F |
T |
T |
|---|
