Regular Expressions
(正規表現)
4th lecture, May 15, 2019
Language Theory and Compilers
http://www.sw.it.aoyama.ac.jp/2019/Compiler/lecture4.html
Martin J. Dürst

© 2005-19 Martin
J. Dürst 青山学院大学
Today's Schedule
- Last week's homework, leftovers
- Minimization of DFAs
- Regular Expressions
- Formal definition
- Conversion to an NFA
- Conversion from an FSA
- Regular expressions in practice
Last Week's Homework 4
都合により削除
Last Week's Homework 1
都合により削除
Last Week's Homework 2
都合により削除
Last Week's Homework 3
都合により削除
Leftovers from Previous Lecture
Today's Outlook
Summary from last time:
- Finite state automata (FSA): deterministic finite automata (DFA) and
non-deterministic finite automata (NFA)
- Regular grammar: left linear grammar and right linear grammar
- All these have the same power, generating/recognizing regular
languages.
Callenge: Regular languages can be represented by state transition
diagrams/tables of NFAs/DFAs, or with regular grammars, but a more compact
representation is desirable.
There is a very powerful way to represent regular languages, called
regular expressions
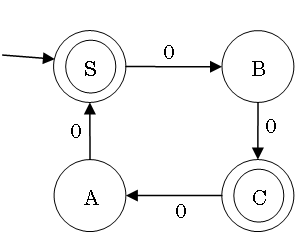
Minimization of DFAs
To create the smallest DFA equivalent to a given DFA:
Overall idea: work backwards
- Separate states into two sets, accepting states and non-accepting
states
- For each state, check which other states are reached for each input
symbol
- Partition each set of states into sets that can reach the same set with
the same input symobls
- Repeat 2. and 3. until there is no further change
Purpose of minimization:
- Efficient (minimum memory) implementation
- Deciding whether two FSAs are equivalent
(they are equivalent if their minimized DFAs are isomorphic)
Example of DFA Minimization
Efficient Implementation of a DFA
State next_state[state_count][symbol_count]; /* state transition table */
Boolean final_state[state_count]; /* final state? */
State current_state = start_state;
Symbol next_symbol;
while ((next_symbol=getchar()) != EOF && /* end of input */
current_state != no_state) /* dead end */
current_state = next_state[current_state][next_symbol];
if (final_state[current_state])
printf("Input accepted!");
else
printf("Input not accepted!");
Application of Regular Expressions
Problem 04C1 of Computer Practice I: Convert &,
", ', < and
> in the input to &, ",
', <, and >, respectively.
One way to write this in Ruby:
gsub /"/, '"'
gsub /'/, "'"
gsub /</, '<'
gsub />/, '>'
gsub /&/, '&'
gsub replaces all occurrences of a give pattern in a string
// are the delimiters for regular expressions (in Ruby, Perl,
JavaScript,...)
Regular expressions match some input.
Regular Expressions
- Expression to denote a set of patterns or words (i.e. a language)
- Very compact
- Widely used, very useful
- Two main variants:
Regular Expressions
- Expression to denote a set of patterns or words (i.e. a language)
- Very compact
- Widely used, very useful
- Two main variants:
(Theoretical) Regular Expression:
Basic Syntax
a: {a} (a single symbol denotes itself)abc: {abc} (concatenation, single word)a*: {ε, a, aa, aaa,...} (Kleene closure)a|b: {a, b} (alternative)- Combinations:
ab|c*|d: {ab, ε, c, cc, ccc,..., d}a(b|c)*d: {ad, abd, acd, abbd, abcd, acbd, accd,...}
More Examples of Regular Expressions
- Combinations:
ab|c*|d: {ab, ε, c, cc, ccc,..., d}a(b|c)*d: {ad, abd, acd, abbd, abcd, acbd, accd,...}
- Number of symbols:
- Even:
(aa)*
- Odd:
a(aa)* or (aa)*a
- Reminder is 2 when divided by 3:
aa(aaa)*
- A specific symbol sequence at the start of a word:
abc(a|b|c)*
- A specific symbol sequence at the end of a word:
(a|b|c)*abc
- A specific symbol sequence in the middle of a word:
(a|b|c)*abc(a|b|c)*
Why Regular Expressions?
- It is possible to use a regular grammar to define a regular language
- A grammar has multiple rewriting rules, and is difficult to
understand
- A single regular expression can represent a whole regular
language.
This regular expression is easy to write and read because it is short.
Notation of Regular Expressions
- Only characters themselves, concatenation, alternative, and repetition
are represented
- "Usual" characters represent themselves
- A small set of characters has a special role (meta-characters:
|, *, (, ), ε)
- Meta-characters may have to be escaped
Formal Definition of Regular Expressions
Theoretical Regular Expressions over Alphabet Σ
| Priority |
Regular Expression |
Condition |
Defined Language |
Notes |
|
ε, a |
a ∈ Σ |
{ε} or {a} |
literals
|
| very high |
(r) |
r is a regular expression |
L((r)) = L(r) |
grouping
|
| high |
r* |
r is a regular expression |
L(r*) = (L(r))* |
Kleene closure |
| low |
rs |
r, s are regular expressions |
L(rs) =
L(r)L(s) |
concatenation |
| very low |
r|s |
r, s are regular expressions |
L(r|s) = L(r) ∪
L(s) |
set union |
L(r) is the language defined by regular expression
r
Caution: Priority
Make sure you understand the difference between the following pairs of
regular expressions:
- abc* vs. (abc)*
- a|b|c* vs. (a|b|c)*
- ab|c vs. a(b|c)
Grammar for Regular Expressions
- Regular expressions also form a language
(set of all regular expressions)
- Grammar: R → ε, R →a, R →b,..., R
→R|R, R →RR,
R →R*, R →(R)
- This is not a regular language, but a context-free language
- The alphabet of a regular expression is the alphabet of the target
language (e.g. a, b,...) and the meta-characters (ε, |, *, (, ))
Regular Expression to NFA
- Construct NFA bottom-up, starting with smallest subexpressions
- Each subexpression is converted to an NFA
- Each subexpression has one start state and one accepting state
- When combining subexpressions, connect start states and accepting states
to form a larger NFA (see next two slides)
- During construction:
- Start state is on the left (no need for incomming arrow)
- Accepting state is on the right (no need for double circle)
- When finished, do not forget to add incomming arrow for start state and
double circle for accepting state
Regular Expression to NFA: Symbols, Alternatives
The NFA for a symbol a has a start state and an accepting state,
connected with a single arrow labeled a (same for ε)
The NFA for r|s is constructed from the NFAs for
r and s as follows:
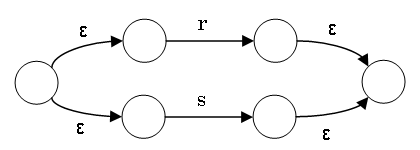
The additional ε connections are necessary to clearly commit to
either r or s.
Regular Expression to NFA: Concatenation, Repetition
The NFA for the regular expression rs connects the
accepting state of r with the start state s through an ε
transition. The overall start state is the start state of r; the
overall accepting state is the accepting state of s.
The NFA for r* is constructed as follows:
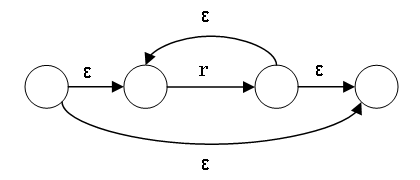
Example of Conversion
Regular expression: a|b*c
In some cases, some of the ε transitions may be eliminated, or the NFA may
otherwise be simplified.
From FSA to Regular Expression
Algorithmic conversion is possible, but complicated
General procedure:
- Create regular expressions for getting from state A to state
B directly for all pairs of states
- Select a single state, and create all regular expressions that pass
through this intermediate state
- Repeat step 2., increasing the number of intermediate states
- Simplify intermediate regular expressions as much as possible (they can
get quite complex)
When understanding what language the FSA accepts, it is often easy for
humans to create a regular expression for this language.
Applications of Regular Expressions
- Many different patterns can be expressed in a compact form
- Clear connection between theory and applications
- Built-in to many programming languages (Ruby,
Javascript, Perl, Python,...)
- Available as libraries in other programming languages (Java, C#,
C,...)
- Usable in many tools (e.g. plain text editors)
- Caution: Theoretical regular expressions and practical regular
expressions differ in many ways
Practical Regular Expressions:
Notational Differences
Practical regular expressions have many additional functions and shortcut
notations
(the corresponding theoretical regular expressions or simpler constructs are
given in parentheses)
.: a single arbitrary character (a|b|c|...)[acdfh]: character class: select a single character
((a|c|d|f|h))[b-f]: shortcut for continuous range in character class
((b|c|d|e|f))- r
+: one or more occurrences of r
(rr*)
- r
?: r or nothing (r|ε, ε
cannot be used in practical regular expressions
- r
{m,n}:
between m and n repetitions of r
(r...rr?...r?)
\*,...: \ escapes meta-characters- Meta-characters:
|*+?()[]{}.\^$
Practical Regular Expressions:
Usage Differences
- Theory: match a full word; practice: match part of a string
^/$ match the start/end of a string or line- The result of the match is not just yes/no, but includes the position of
the match, the substring matched, the substrings before/after the
match,...
- If there are multiple possible matches, the leftmost, longest match is
choosen
(leftmost is more important than longest)
- Parts of a string matching parts of a regular expression in parentheses
can be assigned to variables
- Partial matches can be reused inside the regular expression
Use of Practical Regular Expressions
- Text/document search
- String replacements (single or multiple)
- Cutting strings apart
Notes on Practical Regular Expressions
- Most regular expression engines are more powerful than DFA/NFA/regular
languages
- Most regular expression engines use backtracking
- Some regular expressions may be very slow on some input
Example: String an, regular expression
a?nan (n=3: string:
aaa, regular expression: a?a?a?aaa, really slow starting at , n~25)
- For further analysis, see e.g. https://regex101.com/
Theoretical vs. Practical Regular Expressions
|
Theoretical |
Practical |
| Meta-characters |
* | ( ) |
|*+?()[]{}.\^$ |
| ε |
yes |
no |
character classes ([]) |
no |
yes
|
+, ?, {} quantifiers |
no |
yes |
^, $ anchors |
no |
yes |
| match where |
full word |
part of a string |
Summary of this Lecture
- Regular expressions, regular grammars, and finites state automata all
have the same power to generate/accept regular languages
- Regular expressions are a very compact representation
- DFAs are a very efficient way to implement recognition
- These are very useful for lexical analysis
- However, creating a DFA by hand from a regular expression is tedious
- However, because the number of states is finite, there are languages that
cannot be expressed, e.g. languages with corresponding pairs of
parentheses
Homework
Deadline: May 21, 2018 (Thuesday!), 19:00
Where to submit: Box in front of room O-529 (building O, 5th floor)
Format: A4 single page (using both sides is okay; NO cover page), easily
readable handwriting (NO printouts), name (kanji and kana) and student number
at the top right
- Construct the state transition diagram for the NFA corresponding to the
following grammar
S → εA | bB | cB | cC, A → bC | aD | a | cS, B → aD | aC | bB | a, C
→εA | aD | a
(Caution: In right linear grammars, ε is not allowed except in the rule S
→ ε)
(Hint: Create a new accepting state F)
- Convert the following transition table to a right linear grammar
|
0 |
1 |
| →T |
G |
H |
| *G |
K |
L |
| *H |
M |
K |
| *K |
K |
K |
| *L |
M |
K |
| M |
L |
- |
- Construct the state transition diagram for the regular expression
ab|c*d
(write down both the result of the procedure explained during this lecture
(with all ε transitions) as well as a version that is as simple as
possible)
- Bring your notebook PC (with
flex,
bison, gcc, make, diff,
and m4 installed and usable)
Glossary
- regular expression
- 正規表現
- minimization
- 最小化
- partition
- 分割
- isomorphic
- 同型 (同形) の
- delimiter
- 区切り文字
- alternative
- 選択肢
- repetition
- 繰返し
- meta-character
- メタ文字
- priority
- 優先度
- theoretical regular expressions
- 論理的 (な) 正規表現
- practical regular expressions
- 実用的 (な) 正規表現
- notation(al)
- 表記 (上の)
- arbitrary
- 任意
- leftmost
- できるだけ左



