Finite State
Automata
(有限オートマトン)
Language Theory and Compilers
3rd lecture, May 2, 2025
https://www.sw.it.aoyama.ac.jp/2025/Compiler/lecture3.html
Martin J. Dürst

© 2005-25 Martin
J. Dürst 青山学院大学
Today's Schedule
- Overall schedule
- Summary and homework of last lecture
- Types of grammars
- Finite state automata
- Nondeterministic finite state automata (NFA)
- Conversion from NFA to DFA
Overall Schedule
May 28 (Wednesday), 09:00~10:30
(makeup lecture)
Summary of Last Lecture
- A word over an alphabet Σ is
a sequence of 0 or more symbols from Σ
- A language over an alphabet Σ is
a set of words over Σ
- A grammar is a set of rewriting rules that allow to
produce all words of a language (and only those) by starting from a single
start symbol
- An automaton is a machine that accepts all words of
a language (and only those)
Previous Homework 1
For the language L = { sg, ns, n
},
list the 10 shortest words of L* (in lexicographic
order).
Solution: ε, n, nn, nnn,
nns, ns, nsg, nsn,
sg, sgn
Additional problem (solution voluntary):
List all words of L* of length 4 (in lexicographic
order).
Solution: nnnn, nnns, nnsg,
nnsn, nsgn,
nsnn, nsns, nssg, sgnn,
sgns, sgsg
Previous Homework 2
Using the grammar from the slide
"Example of Grammar and Derivation",
find 3 words produced by that grammar
(different from each other and from ccwwcc).
Give the full derivation for each word
(rule numbers and underlines not needed).
Guess and explain
what language this grammar defines.
Hint: If your guess is not simple,
maybe you have made a mistake.
Previous Homework 2 Solution
[Grammar: S → cwc (1), S →
cPTc (2), R → QPTc (3), T →
QPc (4), PQ → QP (5), cQ →
cc (6), Pc → wc (7), Pw →
ww (8)]
Solution example (partial):
S → cwc
S →cPTc →cPQPTcc
→cPQPQPccc →cQPPQPccc →cQPQPPccc
→cQQPPPccc →cQQPPwccc →cQQPwwccc
→cQQwwwccc →ccQwwwccc →cccwwwccc
S → ... → ccccwwwwcccc
Guess: The grammar defines the language with all the words of the form
cwc,
ccwwcc,
cccwwwccc,...
i.e. cnwncn (n≥1).
Previous Homework 2 (Additional Problem)
Additional problem (solution voluntary): Prove or justify your guess
Example solution summary: The first derivation step will eliminate
S. T will only appear once in any intermediate sequence,
and will later disappear. After using (3) x times (x≥0)
and using (4) one time, there will be a single c on the left,
cx+2 on the right, and a sequence of
x+1 Qs and x+2 Ps in the middle
(c(PQ)x+1Pcx+2
). Using (5), all Qs can be moved to the left, and all Ps
to the right, giving
cQx+1Px+2cx+2.
Then using (7) and (8), the Ps are converted to ws, and
using (6), the Qs are converted to cs, resulting
cx+2wx+2cx+2.
This is cnwncn, with
n=x+2≥2. The case of n=1 is covered
separately by rewriting rule (1).
Today's Schedule
- Overall schedule
- Summary and homework of last lecture
- Types of grammars
- Finite state automata
- Nondeterministic finite state automata
- Conversion from NFA to DFA
Types of Grammars
Grammar types are distinguished
by restrictions on rewriting rules:
(α, β, γ are sequences of
(non)terminals)
Type 0. No restrictions: Phrase structure grammar, (Chomsky) type 0
grammar
Type 1. αAβ →
αγβ, where |α|≧0,
|β|≧0, |γ|≧1:
Context-sensitive grammar (α and β are the
context),
(Chomsky) type 1 grammar
Type 2. A → γ, where |γ|≧1:
Context-free grammar, (Chomsky) type 2 grammar
Type 3. A → aB or A→
a (alternative: A → Ba or
A→ a):
Regular grammar, (Chomsky) type 3 grammar
(for all types, S → ε is also allowed)
Remarks on Homework 2
- All rules except rule (5) are allowed for context-sensitive grammars
(type 1)
- Rule (5) (PQ → QP) is only allowed in a phrase
structure grammar (type 0)
- Rule (5) can be replaced by the four rules
PQ → XQ, XQ → XY, XY
→ QY, QY → QP.
- All these rules are context-sensitive
⇒ this grammar can be made context-sensitive (type 1)
- Languages such as anbnan can
be created
with context-sensitive grammars,
but not with context-free grammars.
⇒ this language is a context-sensitive language
⇒ this language is not a context-free language
Language Type Overview
| grammar |
type |
lanugage type |
automaton |
| phrase structure grammar (psg) |
0 |
phrase structure language |
Turing machine |
| context-sensitive grammar (csg) |
1 |
context-sensitive language |
linear-bounded automaton |
| context-free grammar (cfg) |
2 |
context-free language |
push-down automaton |
| regular grammar (rg) |
3 |
regular language |
finite state automaton |
Regular languages are used for lexical analysis.
Language Type Overview
| grammar |
type |
lanugage type |
automaton |
| phrase structure grammar (psg) |
0 |
phrase structure language |
Turing machine |
| context-sensitive grammar (csg) |
1 |
context-sensitive language |
linear-bounded automaton |
| context-free grammar (cfg) |
2 |
context-free language |
push-down automaton |
| regular grammar (rg) |
3 |
regular language |
finite state automaton |
Regular languages are used for lexical analysis.
Today's Schedule
- Overall schedule
- Summary and homework of last lecture
- Types of grammars
- Finite state automata
- Nondeterministic finite state automata
- Conversion from NFA to DFA
Finite State Automaton Example
(automaton (αὐτόματον) is Greek; plural: automata)
Finite state automata (FSA) are often represented with a state
transition diagram
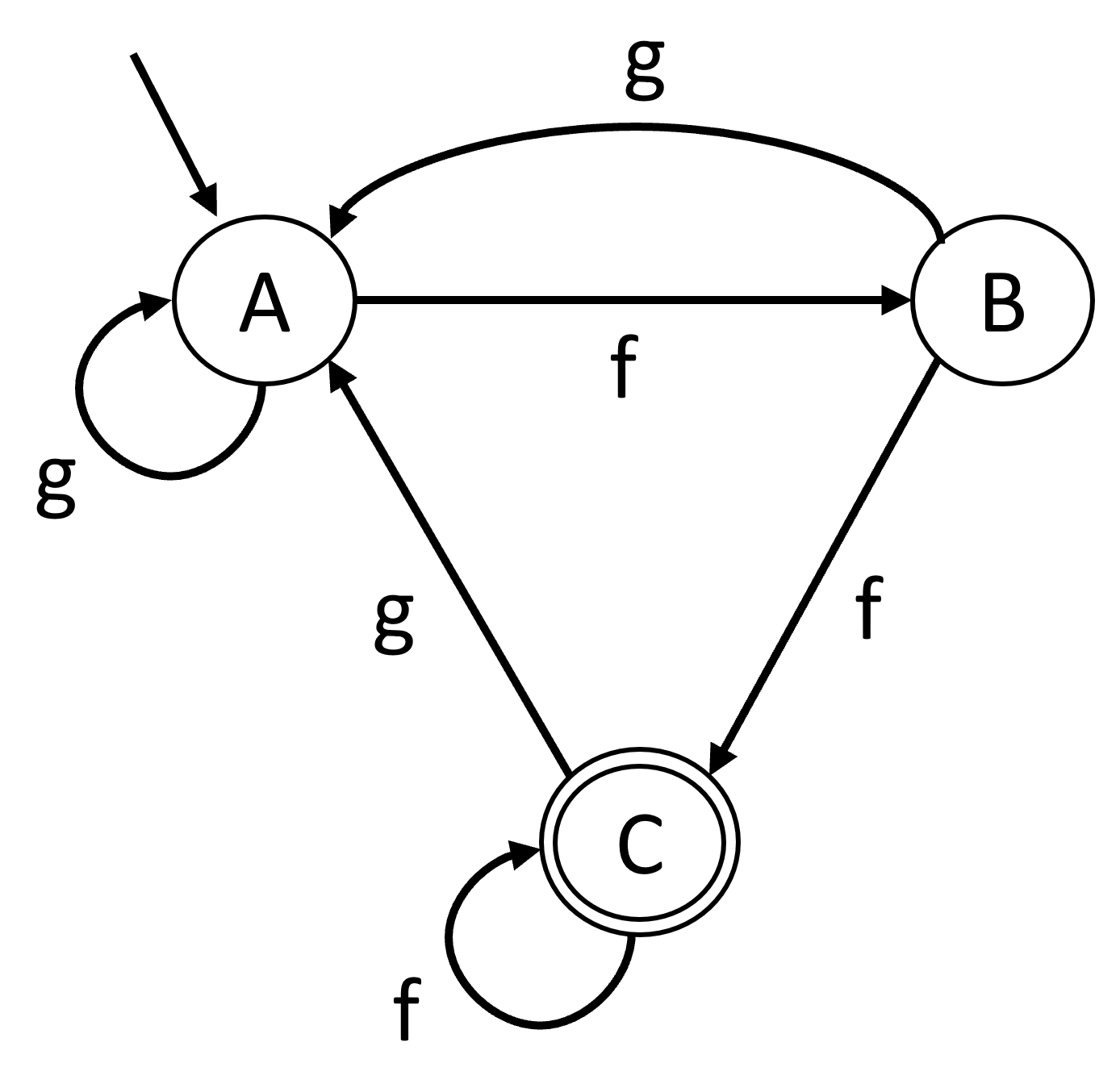
Circles:
states (finite number!)
Arrow from outside:
initial state
Double circles:
accepting state(s)
Arrows with labels:
transitions
Workings of a Finite State Automaton
- Start with initial state
- Repeatedly read one symbol of the input word,
and transition to the next state
along the arrow with the corresponding label
- If the automaton is in an accepting state at the end of the word, the
word is accepted
- If the automaton is not in an accepting state at the end of the word, the
word is not accepted
- If there is no transition with the right symbol, the word is not
accepted
- The number of states is finite
(i.e. there is only limited memory)
Questions

Does the automaton accept ffgfg ? No!
Does the automaton accept fgfff ? Yes!
What language does the automaton accept?
Any sequence of f and g
ending with 2 or more fs.
Examples of Finite State Automata
- Accepting only a word with a single specific symbol
- Accepting words where the number of symbols is odd, or even, or when
divided by 3, the reminder is 2,...
- Accepting words with a fixed sequence of symbols at the start
- Accepting words with a fixed sequence of symbols at the end
- Accepting words with a fixed sequence of symbols somewhere in the
middle
- Accepting words meeting more than one condition at the same time
- Accepting words meeting more than one condition, one after the other
- Accepting words meeting at least one of several conditions
State Transition Tables
Finite state automata can be represented with a state transition
table.
State transition table for our example:
Leftmost column: state
Top row: input symbol
→: start state
(first state if not otherwise indicated)
*: accepting state(s)
Table contents: state after transition
Formal Definition of FSAs
A finite state automaton is a quintuple (Q, Σ,
δ, q0, F):
- A finite set of states Q
(circles in diagram; leftmost column in table)
- A finite set of input symbols Σ
(arrow labels; top row)
- A state transition function δ
(arrows with labels; contents of table)
- An initial state (start state) q0
∈ Q
(circle with arrow from outside; state with arrow)
- A finite set of accepting (final)
states F ⊆ Q
(double circles; states with asterisks)
Today's Schedule
- Overall schedule
- Summary and homework of last lecture
- Types of grammars
- Finite state automata
- Nondeterministic finite state automata
- Conversion from NFA to DFA
Nondeterministic Finite Automata
- An FSA where there is always at most one transition for each input is
called a deterministic finite automaton (or DFA)
- Other FSAs are called nondeterministic finite automata (or
NFAs)
Example of NFA
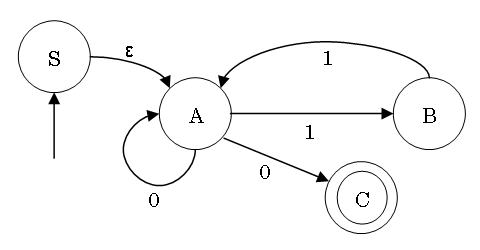
How an NFA Works
- The automaton may be in multiple states (at the same time)
- All transitions for an input are
executed simultaneously, from all current states
- Where there are no transitions,
a state occupation will disappear
- At the end of the input, the word is accepted
if at least one of the occupied states
is in an accepting state
ε Transition
(epsilon transition)
- In NFAs, there may also be some ε transitions
- ε transitions are executed "for free",
i.e. without any corresponding input symbol
- ε transitions are executed
immediately before starting, and
immediately after the "ordinary" transitions
- ε transitions may be executed
in parallel and in succession
- ε transitions increase
the set of occupied states (rather than moving)
- Executing all possible ε transitions
is called ε closure
Comparing DFAs and NFAs
|
Deterministic (DFA) |
Nondeterministic (NFA) |
| concurrently occupied states |
one state |
set of states |
| acceptance criterion |
current state is accepting state |
one of the occupied states is accepting state |
| ε transition |
prohibited |
allowed |
| type of transition function |
δ: Q × Σ
→ Q |
δ: Q × (Σ ∪ {ε})
→ P(Q) |
(there are also NFAs without ε transitions)
Equivalence of DFA and NFA
- NFAs look more complex and powerful than
DFAs
- DFAs seem simpler to implement than NFAs
- Question: Are there languages that can be recognized by NFAs but not by
DFAs?
- Equivalent question: Is it possible to convert
any NFA to an equivalent DFA?
Today's Schedule
- Overall schedule
- Summary and homework of last lecture
- Types of grammars
- Finite state automata
- Nondeterministic finite state automata
- Conversion from NFA to DFA
Example of Conversion
from NFA to DFA
State Transition Table for an NFA
|
ε |
0 |
1 |
| →S |
{B} |
{C} |
{A} |
| A |
{C} |
{} |
{D, B} |
| B |
{} |
{D} |
{A} |
| *C |
{} |
{D} |
{A, B} |
| D |
{} |
{A, B} |
{} |
Conversion from NFA to DFA:
Algorithm Principle
- Set of occupied states of NFA ⇒ state in the DFA
- ε closure of start state of NFA
⇒ start state of DFA
- Set of states of NFA with accepting state(s)
⇒ accepting state of DFA
Summary: Set of States ⇒ State
Conversion from NFA to DFA:
Steps
- Create a transition table for the DFA,
starting with the set of start states
- For each set of states and each input, calculate the set of states that
can be reached
- If there is a new set of states, copy it from the table contents to the
leftmost column, and continue at 2.
- Label all sets of states that contain an accepting state of the NFA as
accepting states of the DNA
- (not necessary) Rename sets of states with new labels
Conversion from NFA to DFA:
Conclusions
- All NFAs can be converted to equivalent DFAs
- All DFAs are (simple) NFAs
- Therefore, DFAs and NFAs
have equivalent recognition power
- Implementing DFAs is very simple,
but the size of the state transition table may grow
(worst case: n → 2n-1 (number of
non-empty subsets of the set of all states); most cases: n →
~2n)
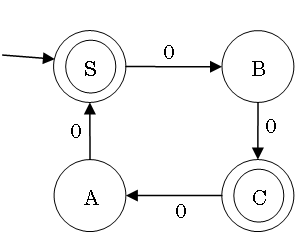
Minimization of DFAs
Task: Create the smallest DFA equivalent to a given DFA.
Overall idea: work backwards
- Separate states into two sets, accepting states and non-accepting
states
- For each state, check which other states are reached for each input
symbol
- Partition each set of states into sets that can reach the same set with
the same input symobls
- Repeat 2. and 3. until there is no further change
Purpose of minimization:
- Efficient (minimum memory) implementation
- Deciding whether two FSAs are equivalent
(they are equivalent if their minimized DFAs are isomorphic)
Example of DFA Minimization
Efficient Implementation of a DFA
/* state transition table */
State next_state[state_count][symbol_count];
Boolean final_state[state_count]; /* final state? */
State current_state = start_state;
Symbol next_symbol;
while ((next_symbol=getchar()) != EOF && /* end of input */
current_state != no_state) /* dead end */
current_state = next_state[current_state][next_symbol];
if (final_state[current_state])
printf("Input accepted!");
else
printf("Input not accepted!");
Today's Summary
- Finite State Automata (FSAs) are the tool to accept/reject words of
regular languages
- Both Deterministic Finite Automata (DFAs) and Nondeterministic Finite
Automata (NFAs) recognize the same (class of) languages
- DFAs allow efficient inplementation of recognition
of regular languages
- This can be used for lexical analysis
Challenge (for next lecture): DFAs and NFAs have complex descriptions. Are
there simpler descriptions of regular languages?
Previous Homework 3:
Cygwin Download and Installation
(no need to submit, but contact me by e-mail
if you have any problems)
Install cygwin on your notebook computer
(detailled
instructions with images).
Make sure that you select/install gcc (gcc-core),
flex, bison, diff (diffutils), make, and
m4 .
If you have an earlier cygwin installation,
make sure to check/update.
Checking flex, bison, gcc,...
Installation
Start up a Cygwin Terminal session.
Check each software with the following commands:
flex -V (V is upper case)bison -V (V is upper case)gcc -v (v is lower case)diff -v (v is lower case)make -v (v is lower case)m4 --version
Homework Submission
Deadline: May 7, 2025 (Wednesday), 18:40
Format: A4 single page (using both sides is okay; NO cover page, portrait
orientation), easily readable handwriting (NO printouts), name (kanji and kana)
and student number at the top right
Where to submit: Box in front of room O-529 (building O, 5th floor)
Homework
- Draw a state transition diagram for a finite state automaton that
recognizes all inputs that (at the same time)
- Start with qt
- End with tq
- Contain an even number of h
- Contain no other symbols than q, t, and
h
- Draw the state transition diagram for the NFA in the state transition
table below
| |
ε |
O |
l |
| →S |
{P} |
{Q} |
{E} |
| E |
{} |
{P} |
{P, T} |
| P |
{} |
{T} |
{} |
| *Q |
{P} |
{} |
{S} |
| T |
{} |
{E, P} |
{Q} |
- Create the state transition table of the DFA that is equivalent to the
NFA in homework 2 (do not rename states).
- Check the versions of
flex, bison,
gcc, diff, make, and m4
that you installed (see slide 4, no need to submit, but contact me by mail
if you have a problem)
Glossary
- Finite state automaton (FSA)
- 有限オートマトン
- deterministic finite automaton (DFA)
- 決定性有限オートマトン
- Non-deterministic finite automaton (NFA)
- 非決定性有限オートマトン
- regular grammar
- 正規文法
- state transition diagram
- 状態遷移図
- transition
- 遷移
- initial/start state
- 初期状態
- accepting/final state
- 受理状態
- accept
- 受理する
- finite
- 有限
- state transition table
- 状態遷移表
- state transition function
- 動作関数
- simultaneous(ly)
- 同時 (な・に)
- ε transition
- ε 遷移
- ε closure
- ε 閉包
- equivalence
- 同等性
- renaming (of states)
- 状態の書換え




